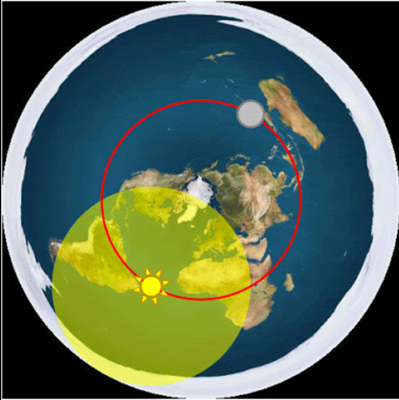
Globebusters - promoting Torque the Line experiment
Dear Readers,
Professional engineer Brian S. Dobbs, PE provides an extremely detailed and complete evaluation of this experiment, as proposed by Mitchell of Torque the Line. We have included it in full so that we can all learn what factors need to be considered and understood in order to do this experiment properly.
(See the bottom section of this article.)
- - -
The folks at Globebusters once again want you to spend more of your money. This time for the flat Earth experiment "Torque the Line" to be performed by Mitchell Stinson in Australia.
Mitchell Stinson is not (pro flat-Earth) or (pro globe-Earth) at this point.
What are they trying to prove?
"Having some sort of strong line stretched between two shores, and the pulling that line taut and seeing if the line enters the water – if there is a hump like we’re told."
https://www.youtube.com/watch?v=e9dewQprEDk


Our evaluation:
The experiment as proposed is critically flawed.
Once the braded line hits the water it is not possible to theoretically/mathematically know, by how much the line should sag. Catenary Curve calculators deal with a line suspended in mid air - not touching anything and not immersed in water or other liquids.
There is no below water Catenary Curve calculator, because too many variable external factors come into play.
The displacement and amount submerged figures presented by Mitchell in the video are his alone - and he does not show the detailed calculations of how they were derived.
Furthermore, to minimize the effect of external forces (wind, water, water current, etc.) influencing the experiment results, a heavy line or chain is suggested. Not a light weight fishing line that has the ability to float*.
*[Note: "Braided line, or so-called superlines, float and perform well for spinning reels or on “professional grade” baitcasters."
http://guide.sportsmansguide.com/tips/braid-vs-fluorocarbon-vs-monofilament/]
In general...
A line of 5-km length (16,404-feet) will definitely sag.
The experiment as proposed by Mitchell (dipping into the water) can acknowledge the sag, but will not in any meaningful way be able to know with certainty what the correct amount of sag in water should be.
Our Suggestion:
Do the Catenary Curve experiment from shore to shore, but raise the spectra braided line high enough so that it never touches the water. Mark the center of the line with paint or some other identifier. Measure the height of the line above the water at each of the two shore positions. Then adjust until they are both the same. Pull the line as taut as possible and secure it from movement. Then go by canoe out to the center of the line over the lake, and measure how high above the surface it is there.
Line sag = height of the line above the water at the shore - the height of the line above the water at the middle location.
Detecting any amount of sag proves that gravity is acting on the line.
But is there a curvature bulge?
You can now find out. Based on your measured cable tension, plug the numbers into the Displacement Cable Sag Error Calculator. The difference between your measured sag and that calculated number is due to Earth curvature bulge.
BUT DO ALL OF THIS IN MID-AIR WITHOUT TOUCHING WATER.
- - - - - - - - - -
Their sample calculations:


- - -

More discussion of the problems with the experiment as currently outlined:
Basing this test on water, wind, waves and spectral braid line buoyancy, is a very doggy proposition. It's not clean and will always leave the door open to multiple interpretations. Calculating the total buoyancy effect (for only the portion of the 2.77 mile braid that actually is in the water) - and how that changes the total tension on the entire line when water is moving, is a fool's errand.
Weight and buoyancy ALREADY both depend upon the strength of the gravitational force acting on them.
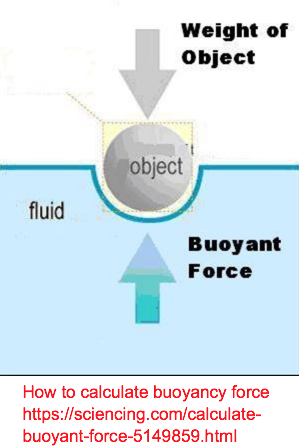

Placing any part of the spectral braided line in the water, invalidates the use of the Displacement Cable Sag Error Calculator.
The Displacement Cable Sag Error Calculator has four math variables:
1. Cable tension - must be measured during the experiment itself
Note: once the braided line lays in the water this value (cable tension) is indeterminate, and the calculator can no longer be used
2. Straight line distance - a known item
3. Cable weight per unit length - a known item
4. Force perpendicular to the cable length = a known item, the force of gravity
Since the cable tension applied is not known until measured during the experiment, all sag numbers presented by Mitchell in this video are subject to change.
For the above proposed experiment:
straight line distance = 2.77 miles = 14,625.6 feet
cable weight per unit length (pounds per foot) = 0.93 pound / 5,000 meters or 16404.2 feet = 0.00005669 pound / foot
force perpendicular to cable length = 32.18503937 ft/sec/sec
- - - - - - - - - -
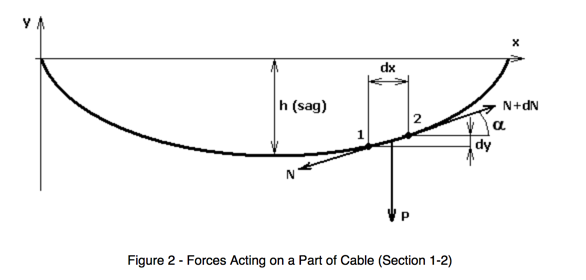
In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends, due to the force of gravity acting on it.
Here is an example of the Catenary Curve...

How is the curve calculated?
The following calculator can be used to determine the displaced cable length and the amount of cable sag, due to Earth's gravity...
https://www.spaceagecontrol.com/calccabl.htm
- - - - -
Added on October 1, 2018...
Greetings Mitchell,
1) adding concrete to the 60-liter container means that the buoyancy force is no longer 60 kg upward.
What is the weight of the concrete that you are going to put in it?
2) a Catenary Curve calculator is not applicable for under water use. Therefore, it cannot be used to determine sag in your experiment.
3) show here the fluid dynamic calculations that you will use to determine braid line sag.
4) so your braided line is buoyancy neutral. You should use buoyancy negative if you want it to sink and properly get sag.
5) rather than calculate or use the manufactures table on braided line buoyancy, you should soak at least 100ft of line in water for several hours, and then measure it yourself.
6) from a logistics standpoint, if you stretch a line (above or just below the water surface) over hundreds of yards, that poses a sever risk to swimmers and especially boaters. Your thin line above water may not be seen by boaters, resulting in decapitation or sever personal injury. The lake needs to be completely clear of people where you conduct the experiment.
7) You mentioned that your test is also about gravity. Well, the buoyancy force is gravity dependent. If you accept the buoyancy force calculation than you have already accepted g = 9.8 meters/sec/sec acceleration value.
- - - - -
Here is their request for money...
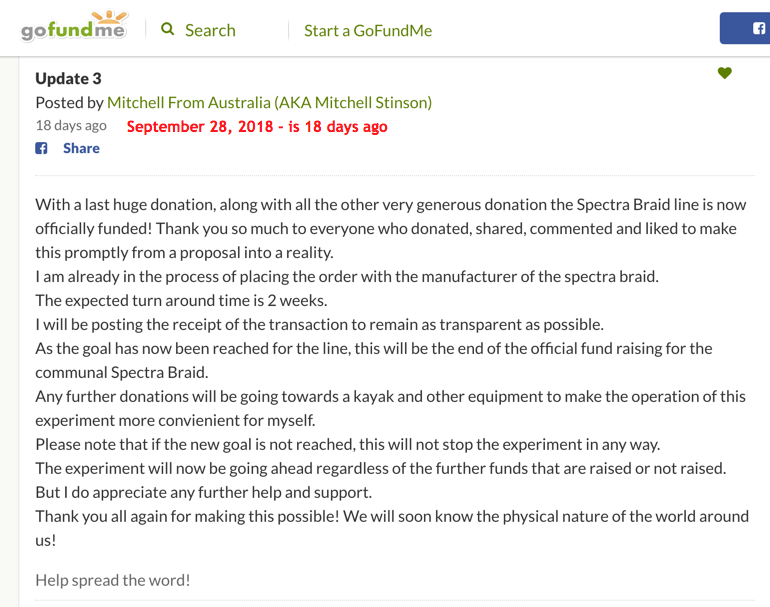
TORQUE THE LINE EXPERIMENT
This is not a Flat Earth Experiment, or a Globe Earth Experiment, it’s a first of its kind test to determine the nature of the world we all live in.
(GOAL IS $900 FOR SPECTRA BRAID LINE TO START EXPERIMENT, ANYTHING EXTRA IS A CONVENIENCE FOR CANOE AND REEL)
The first ever Experiment that can physically measure the curvature of the Globe Earth, or the lack of it. As it stands we only have observational experiments involving optics, lasers, cameras and theories.
Put all pre-conceived ideas aside and help prove something that has not adequately been proven.
This gofundme is to pay for a 5km length of Spectra Braid line, which is the most vital piece of the experiment. All other equipment expenses I am covering myself.
This is an experiment funded by the community, so it will be available for the community. After the completion of my experiment, I am making the line available to whomever wants to also replicate the experiment for themselves. After all, no one single result can make an objective truth, it is the combined results of the same experiment repeated in multiple locations with the aim of proving the last results wrong.
Funds raised will go towards the cost of the Spectra Braid line, which including postage costs $900AU, straight from the manufacturer. Anything raised above this amount will pay for a kayak/canoe($700) as I only have an inflatable boat or surfboard to use at the moment. Then possibly a reel ($510)for the line, as you can imagine reeling in miles of line neatly will be a challenge.
All other equipment cost I am covering myself.
Please, be a part of history and make this happen. If you can’t donate money, donate your time to sharing the experiment anywhere and everywhere you can, online, in your local community, tell your mum, dad, sister, cousin, etc, every person that knows about this test and it’s results will know that little bit more about the place that we live in.
For all the info visit YouTube and search for “Torque the line experiment” the YT channel Or email me directly at This email address is being protected from spambots. You need JavaScript enabled to view it.
- - - - -
For Bob Knodel and his Globebusters gang, shown below is what it's really all about. There is nothing wrong with the science and photographs that prove the Earth is a rotating sphere...

- - -
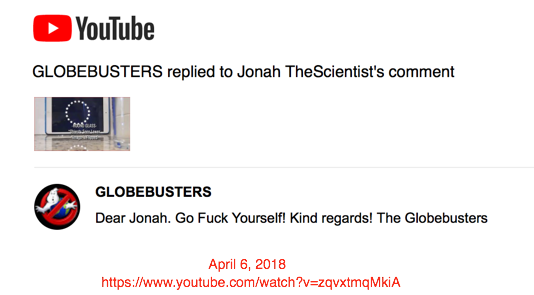
Bob Knodel gets nasty...
- - -
Jeran from Globebusters wanted to do the same experiment. He advertised a date and time for it, but he didn't show up and so the experiment never happened...
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
A professional engineers view point...
The following Torque the Line experiment review and critique, by Engineer Brian Dobbs, was sent to Mitchell, who considered it carefully.
October 1, 2018
Dear Mitchell Stinson,
I am a registered professional engineer in the United States. I started following the resurgent flat Earth “movement” online over a year ago, and not because I think the Earth is flat. I’ll be perfectly honest with you; my intrigue with this topic stems from the satisfaction that I get from listening to the ignorance, delusion, and sanctimony of the “thought leaders” that are creating most of the online content. Having said that, I also enjoy investigating their “proofs” and looking into the science and engineering principles that explain what they think they are seeing. It offers me an opportunity to keep my knowledge base sharp and, admittedly, to learn new things. Consequently, I also have a soft spot for citizen-sponsored science, which is why I am taking an interest in your “Torque the Line” experiment.
I will be forthright: this is not a good experiment. I have watched your videos and listened to your interviews, and I see that you do not understand how complex an undertaking it will be. Deriving anything useful from measuring inches of deflection in a fishing line that is several miles long across an open body of water is not something you can just do without careful preparation. Nonetheless, I must admit that I cannot think if a specific reason why this test should fail if you did it carefully. My objective in preparing this critique for you is to empower you to have the best possible chance of performing a conclusive experiment. You claim to “only be interested in the truth”, and if that is true then you must perform this experiment carefully, document your process thoroughly, and report your findings honestly.
There are aspects to this project that you didn’t think of. Moreover, there are aspects that I can’t think of either. That is why the process of peer review is vital. You must seek comment from outside the echo chamber of flat Earth fanaticism. Since you did not do that, I will do it for you. I will be sharing your experiment and my critique on the skeptic website Metabunk and possibly others. In the chance that somebody there offers you their thoughts, please carefully consider them.
Mitchell, the Earth is not flat. You may believe that statement makes me a “fanatical, indoctrinated globe-Earth sheep” or whatever, but I am no more fanatical about Earth’s shape than you are “fanatical” about your belief that you are reading this sentence right now. These are facts: The Earth is a planet, it orbits the sun, in the vacuum of space, and gravity is real. Their validity is not contingent on your beliefs, or mine. While I get a lot of kicks out of listening to Jeran, Mark Sargent, Bob Knodel, David Weiss, and the others make fools of themselves on YouTube, I honestly cringe to think about how they will be judged in a year or two when this “movement” is over. You don’t have to go down with them! I implore you to sharpen your judgment and critical thinking skills. Honestly investigate the established sciences. Take a physics class, preferably one with a laboratory component where you can observe for yourself that the laws of physics weren’t made up to “indoctrinate” you.
I wish you the best of luck with your experiment. You’re going to need it. I look forward to scrutinizing your results.
Best regards,
Brian S. Dobbs, PE
- - -
TORQUE THE LINE EXPERIMENT: A CRITIQUE
October 1, 2018
BACKGROUND AND STATED HYPOTHESES
Mitchell Stinson of Australia has started a campaign on the fundraising website GoFundMe to conduct an experiment that he is calling “Torque the Line”. As of September 29, 2018, the campaign raised $935 versus a $2,000 target, donated primarily by believers of the newly resurgent notion that the Earth is a flat plane and that the natural phenomenon of gravity, a concept that has played a central role in nearly all lines of inquiry within the physical sciences for the last several millennia, does not exist. Stinson does not openly state his opinion on the matter, but his experiment is being promoted on podcasts and YouTube channels that are openly affiliated with “the Flat Earth Movement”. Stinson himself has also openly appeared on many of these programs. Nonetheless, on the experiment’s GoFundMe page, Stinson claims:
“This is not a Flat Earth Experiment, or a Globe Earth Experiment, it’s a first of its kind test to determine the nature of the world we all live in.”
Stinson explains on his YouTube channel that the experiment aims to test whether the shape of the Earth is spherical by placing a fishing line across a body of water with both ends level with the water surface, and then applying tensile stress to the line (or “Torqueing” it, as Stinson misuses the term)1. Stinson reasons that if the Earth is spherical, then the stressed line will have less curvature than the surface of the water and will therefore drop below the surface. On the YouTube video titled “Torque the Line – Introduction”, Stinson offers the following general diagram:

--------------------------
1 Two versions of the experiment are presented, one in which the line is completely out of the water across the entire span, and one where the line is at or below the surface of the water for the entire span. Stinson dedicates almost equal parts of his presentations to the former variation, but states early in the Introduction video that such a test is not feasible due to catenary line sag. Since that variation of the experiment is unfeasible by Stinson’s own admission, it is ignored in this analysis.
A Critique of the Experiment
Both settled science and the believers of the flat Earth conjecture agree that flat Earth and gravity are mutually exclusive concepts. If one is real, then the other is not. In its essence, this experiment is a test of whether gravity is real. Stinson’s central claim is that a submerged line-under-tension, which spans a long distance near the surface of a body of water, can be used to determine whether gravity affects the shape of the water’s surface.
Stinson approaches the experiment with little scientific formality. He does correctly identify many of the factors that would affect the outcome, he exercises some rigor in applying scientific concepts, and he attempts some calculations to predict an outcome. However, an experiment requires a testable hypothesis, and of this test Stinson claims little more than the following:

(The “curve” being the profile of the spherical Earth.)
This statement does little to serve as a falsifiable basis for experimentation. How much submergence must be observed for a definitive conclusion? Does Stinson claim that, if the line is submerged by any measurable amount at any location, then gravity is real and the Earth is spherical? Stinson understands that buoyancy will affect the results of the test, but an object must be at least partially submerged in order to even be buoyant! By leaving vague the criteria for a definitive evaluation, Stinson has invited misinterpretation of the results and ambiguity in any conclusions drawn.
Another concern is that Stinson does not hypothesize what the shape of a positively-buoyant submerged line will take. Further, Stinson is heard on YouTube channels openly claiming that, since the line is buoyant, then the line is “supported at all parts”, and its shape will not be a catenary curve. The shape a positively-buoyant submerged line will be an inverted catenary curve. Stinson cannot make a valid hypothesis without understanding this.
Analysis of Experiment Design
In the experiment’s introduction video, Stinson states that he intends to use 50 lb.-test line made of high molecular weight polyethylene (HMPE) produced by Honeywell under the material name Spectra. Spectra is marketed as fishing line, among other products, under the brand names PowerPro, FINs, and Tuf-Line. Stinson has chosen two possible sites to conduct the test, a salt-water lake with a 2.2-mile
section of open water between shores, and a fresh-water canal with a 2.77-mile straight run available to conduct the test. Of the design, Stinson is encouraged to consider the following:
• Line Tension. For his calculations and his experiment design, Stinson assumes that the line tension will be equal to the breaking strength of the line: 71 lbf. This tension is not possible to achieve because, as the name implies, it would break the line. Stinson is encouraged to research the difference between yield strength and ultimate strength. A state of stress that exceeds the material’s yield strength will change the properties of the line and invalidate the underlying assumptions of the stated hypothesis. For the experiment, Stinson is strongly encouraged not to exceed the test-rating of the fishing line.
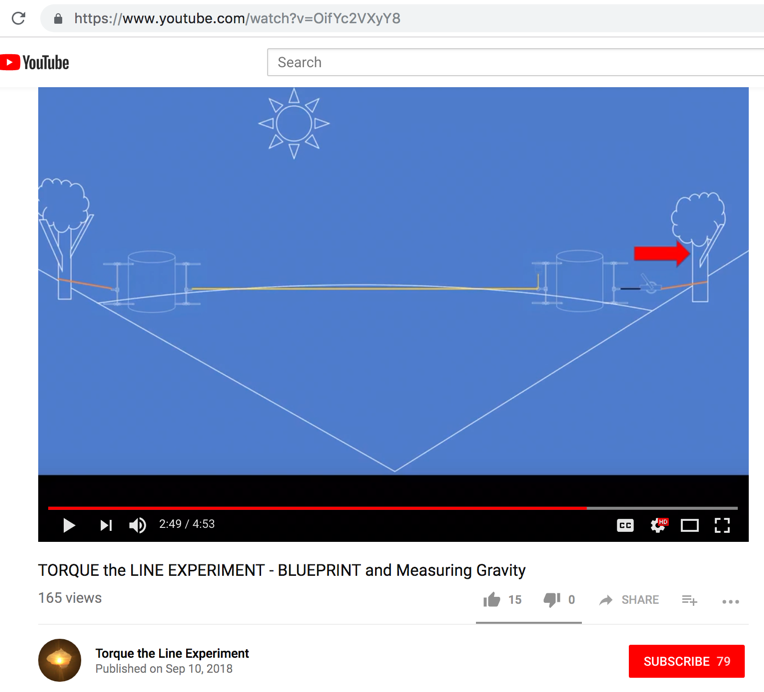
• Anchor design. Stinson provides a qualitative illustration of the anchor design in the YouTube video “TORQUE the LINE EXPERIMENT – BLUEPRINT”. The design is based on a 60L barrel counterweighted by water with concrete at the bottom, and is shown below:
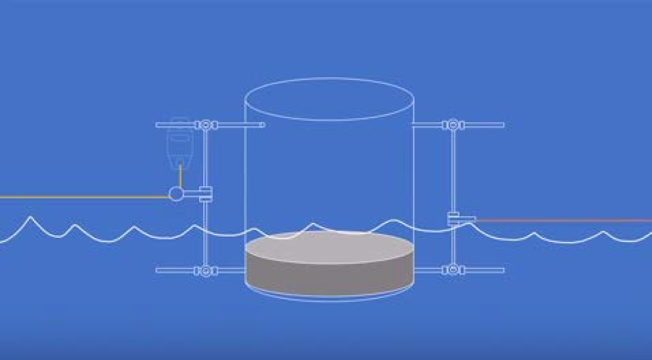
In the above illustration, the experimental line is shown in yellow on the left, while the orange line represents a chain that will attach to a tree or other fixed anchor point via a come-along. The come-along is used to apply tension through the apparatus to the test line. One wonders why the come-along, tension dynamometer, and fixed anchor cannot all simply be in-line; since the tension is expected to be transferred through the anchoring apparatus, any attempt to ballast the apparatus will only increase the friction below it, increasing the required tension in the chain and destabilizing the barrel.
Furthermore, since the dynamometer is separated from the test span by the pulley, the pulley friction becomes a source of measurement error.
Finally, this method is inadequately prepared to handle the fact that applying over 50 lbf to 2.2 miles of the selected line will result in strain elongation of over 300 feet.
Stinson further explains that the anchors are designed to be partially submerged in water, which makes the choice to use water as the ballasting medium a very curious one.
• Measurement of Line Depth. Stinson make no mention of how he intends to measure the depth of the cable. By his own calculation, Stinson predicted that for the 2.2-mile test at the salt water lake, the line depth at the midpoint of the line could be as little as 5” (this claim is dubious, as explored in the following section). Given that the amplitude of undulation of the water’s surface could approach that value, even on a calm and windless day, one wonders how an accurate measurement is even possible.
Analysis of Calculations
Stinson made the following predictions:
• Salt Water Lake: For a 2.2-mile span, a spherical Earth with a nominal radius of 3959 miles should have a “bulge” of 9.68” versus a straight chord. The middle of a line at that span will be displaced upward by buoyant forces by 4.46” versus a straight line between the cable endpoints. Therefore, the middle of the cable would be submerged by 9.68” – 4.46” = 5.22”.
• Fresh Water Canal: For a 2.77-mile span, a spherical Earth with a nominal radius of 3959 miles should have a “bulge” 15.35” versus a straight chord. The middle of a line at that span will be displaced upward by buoyant forces by 1.8” versus a straight line between the cable endpoints. Therefore, the middle of the cable would be submerged by 15.35” – 1.8” = 13.55”.
Stinson has not made his calculations available for review. However, in the YouTube video titled “Spectra Braid Line Specs – Torque the Line Experiment”, Stinson shows a screen capture of a spreadsheet presumably authored by Stinson. It shows line weight, buoyant force, and line lift, but the source calculations are never revealed and therefore cannot be verified (in one instance in “Spectra Braid Line Specs - Torque the Line Experiment” timestamp 4:06, the line lift is the active cell, but the formula bar reveals that that the number is just an entered value, not a calculation). However, some observations can be made from the video:
• Calculation of Line Deflection due to Buoyancy. Stinson is shown in the video using an online line sag calculator which is based on a catenary curve calculation. The calculator is made available at a website titled SpaceAge Control, and its calculations were verified to be correct. The calculator is shown with values for the unworkable out-of-water variation of the experiment pre-populated in the calculator inputs. It is unknown whether the calculator was also used to predict line deflection due to buoyancy for the fully-submerged variation, but the values shown in the YouTube videos and in the spreadsheet for that parameter could not be re-created in the calculator.
Stinson makes an incoherent assumption about what shape the line will take when submerged. He states that the line will be “neutrally buoyant”, possibly meaning he thinks the line will be straight, but he also predicts there will be “line lift” due to buoyancy. Obviously both statements cannot be true.
Nonetheless, the calculation methodology for line deflection due to buoyancy could not be verified, nor could the calculated value be recreated with the referenced calculator, known laws of physics, or known engineering methodologies.2
• Units Analysis. Stinson uses units of measurement that are incorrect for the parameters he is representing, namely he substitutes “mass” for “weight”. Stinson starts with a calculation of the line’s mass based on the volume multiplied by the manufacturer’s stated Specific Gravity (0.98 g/cc). The calculations of the forces of weight and buoyancy are then carried through in units of mass. The weight of the line is given in grams (a unit of mass). The so-called “weight of buoyancy” is also given in grams. His conversion from SI to US systems of measurement are also dubious; no distinction is made between pounds force and pounds mass. To his credit, Stinson is not the first person to interchange the concepts of mass and force, as the two are routinely conflated in day-to-day life. It is possible that he could have “gotten lucky” by computing numerically accurate equations while being completely naïve to the distinction (something that he would also not be the first person to do, even among seasoned engineers and scientists). However, proper application of these concepts is vital to accurately predicting the outcomes of this test, and thus establishing criteria for meaningful conclusions. Given that Stinson has not made his calculations available for review, his “luck” cannot be determined.
New Calculations
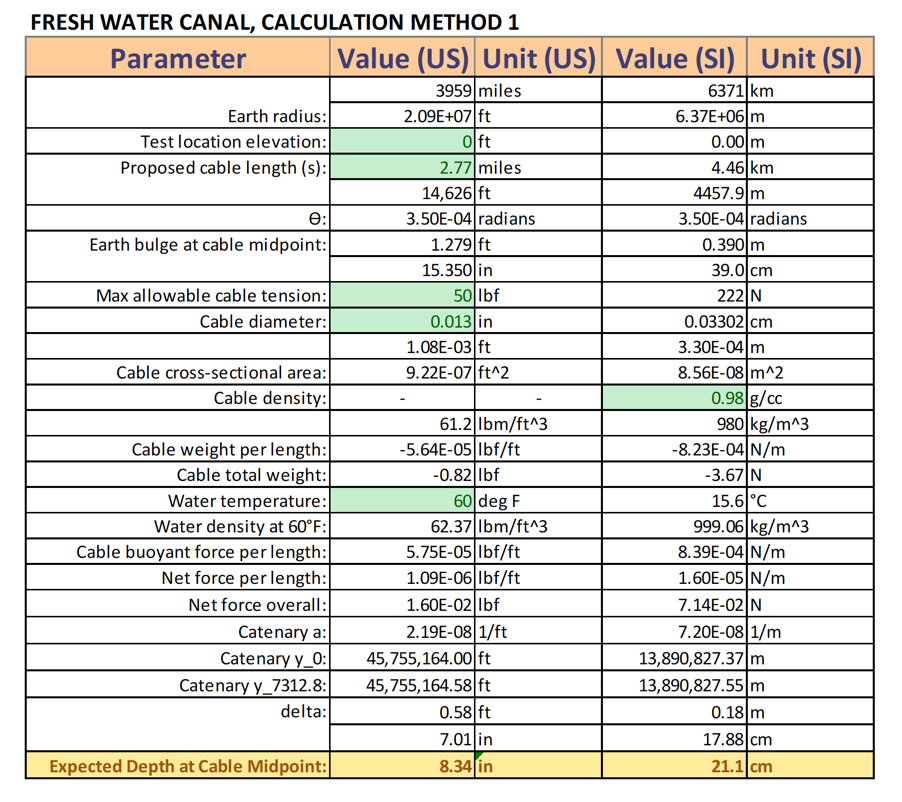
The following are calculations for line deflection due to buoyancy and expected depth, using the manufacturer’s stated properties for the Spectra cable. Two calculation methodologies were used, and are described below:
Calculation Method 1
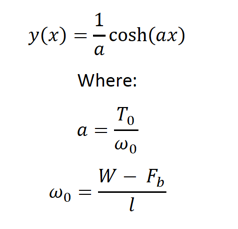
Assumptions:
1. Line properties provided by manufacturer are accurate.
2. The line is inelastic and cannot transmit bending or torsional moments
3. If the line is completely submerged, is in a state of tensile stress, and the buoyant force acting on the cable is higher than the weight of the cable, then the cable will assume the shape of an upward-curving catenary curve of the form:
--------------------------
2 It is clear from the video that Stinson understands that gravity is used in the calculation of both weight and buoyancy. It is not stated whether he intends to provide a new model for these phenomena if his experiment disproves the existence of it.

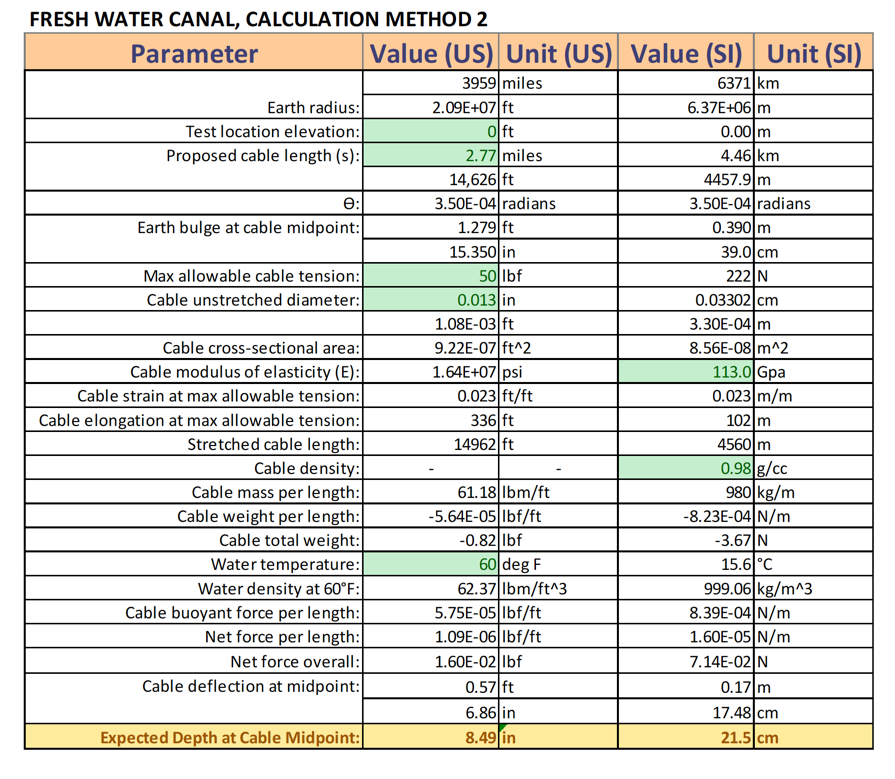
Calculation Method 2:
Assumptions:
1. Line properties provided by manufacturer are accurate.
2. The line is elastic. Stretch in the line reduces its weight and volume per length
3. The shape of the submerged line will be an inverted catenary, as in Method 1, but the shape can be approximated by a parabola (Bowden, 2004), and the mid-span deviation from a straight line can be approximated as the first term of a power-series expansion of the function cosh(u) about the midpoint, which gives:

Universal Assumptions:
1. Earth is a sphere with a mean radius of 3,959 miles.
2. Gravity is real.
3. In Earth’s gravitational field, the surface of bodies of liquid assume a homogeneous gravitational potential
4. For the selected test locations and for measurements in the scale of this experiment, the gravitational effects of other celestial bodies such as tidal effects are assumed negligible.
5. A surface of homogeneous gravitational potential will exhibit a “bulge” between any two points compared to a straight-line chord between those two points.
6. If a line or cable is strung between two points on the surface of body of water on Earth, and the distance between the two points is sufficiently large, and the tension in the line or cable is sufficiently high, then the line or cable will be completely submerged for the entire span.
7. The line tension shall be increased until the horizontal force in the line is equal to the manufacturer’s stated test rating (50 lbf).
8. T0 = T for small angles at the anchor points
9. Water temperature is 60°F.
10. Experiment locations are at an elevation of 0 ft. above sea level.
11. The properties of water at the salt water lake test site are equal to ocean water
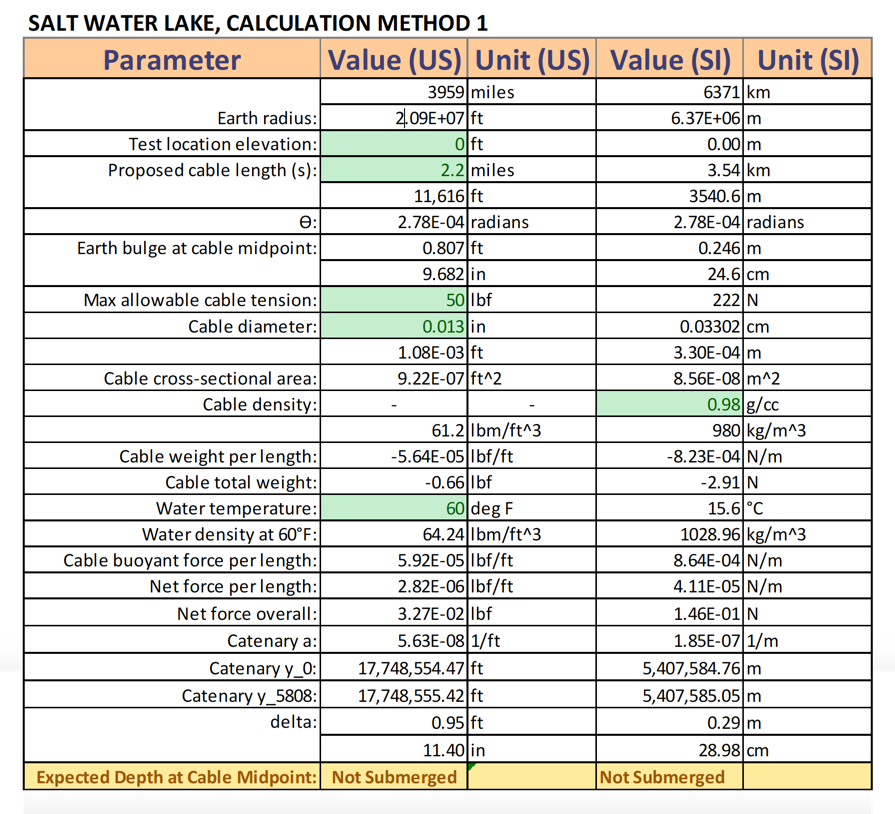
Results Green cells are inputs
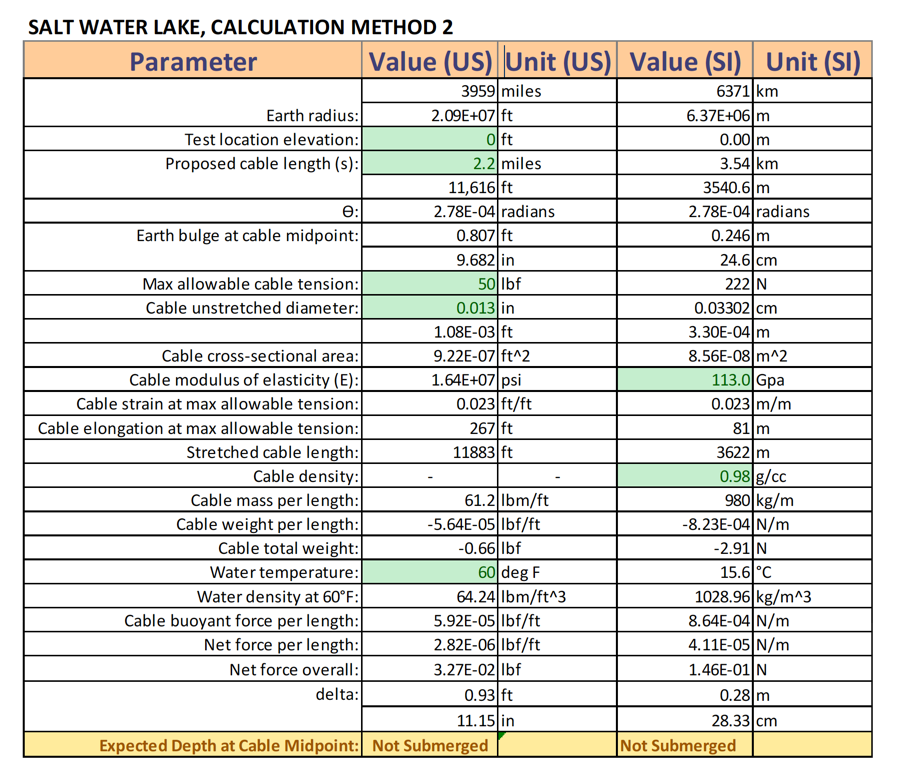
Green cells are inputs
Green cells are inputs
Green cells are inputs
Analysis and Conclusions
Both calculation methods indicate that it is not feasible to conduct the test in salt water. At T = 50 lbf, the buoyant force is high enough to hold the cable at the surface of the water. For the fresh water canal, calculation method 1 predicts that line is should be at a depth of 8.34”, while method 2 predicts a depth of 8.49”.
Considerations
Stinson is encouraged to consider the following:
1. For any results to be considered legitimate, Stinson must develop a falsifiable hypothesis that is based on analytical prediction.
2. The calculation of line depth is highly sensitive to the assumed density of the line. A reduction in assumed specific gravity of just 0.01 g/cc changes the calculated cable depth by 74%! 0.98 g/cc is shown on most online product data, which is the value used in both these and Stinson’s calculations. However, Honeywell publishes conflicting information about the density of Spectra fiber. In a Spectra product data sheet published in 2008, the density of Spectra is reported as 0.97 g/cc (the data sheet can be found here: http://www51.honeywell.com/sm/afc/common/documents/PP_AFC_Honeywell_Spectra_fiber_2000_Product_information_sheet.pdf). Stinson is strongly encouraged to measure the density of the test article for himself, using NIST- OR NMI-certified instruments, and to declare his method for doing so. Furthermore, Stinson is strongly encouraged to perform uncertainty and error-propagation analyses for this parameter.
3. Related to the density, the calculation is also extremely sensitive to the assumed diameter of the line. Again, line manufacturers publish conflicting data for this parameter. For PowerPro-brand braided Spectra line in 50 lb.-test, online retailer FishUSA reports that the line thickness is 0.013 in and 0.36 mm (source: https://www.fishusa.com/product/PowerPro-Braided-Spectra-Fiber-Line). However, these two values are not equivalent; 0.013 in is equal to 0.3302mm, not 0.36mm. The difference, 0.0302mm, changes the calculated depth by over 16%. Moreover, customer reviews of the line claim that the advertised diameter is inaccurate. The following review was found on the FishUSA website for PowerPro-brand braided Spectra line:
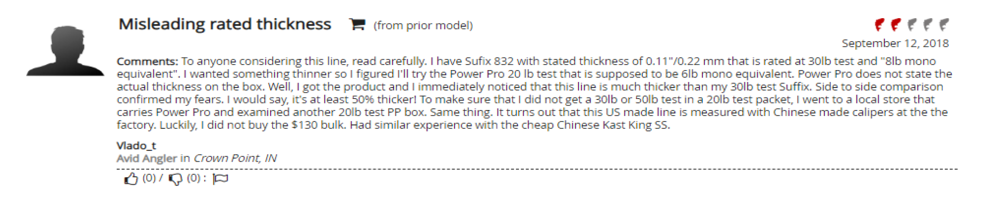
Stinson is strongly encouraged to measure the diameter of the test article for himself in several places along the line using NIST- OR NMI-certified calipers. Furthermore, Stinson is strongly encouraged to perform uncertainty and error-propagation analyses for this parameter. Finally, for this test the buoyant force is proportional to the volume of the line under tension, which is
likely to be different than the volume without tension. In his book Wire Ropes, K. Feyrer reports on the reduction of rope diameter due to rope tensile force as follows:
The length-related compressive force first results in resetting any loose wires and strands and then in deforming the rope in a different way. There is also some minor deformation due to the pressure between wires crossing. As far as fibre-core wire ropes are concerned, a large diameter reduction occurs and this is mainly due to the compression of the core. (Feyrer, 2015).
Stinson should repeat his measurement of line thickness while the line is under a state of stress and report his method for doing so.
4. The calculation is sensitive to water density and, consequently, water temperature. Every 1°F change in water temperature results in a change in submerged depth of .030in. Stinson is strongly encouraged to directly measure the water density at the test site using certified instrumentation, and to report his method for doing so. The test date, time, weather, and air and water temperature should also be reported.
5. Stinson absolutely must develop a method for accurately measuring the depth of the submerged line that normalizes for the surface undulations that are typical for a large body of water. Waiting for a windless day is a given. Another suggestion would be to use a large, thin block of a very buoyant material such as Styrofoam with a scale adhered to the side, as shown in the following figure:
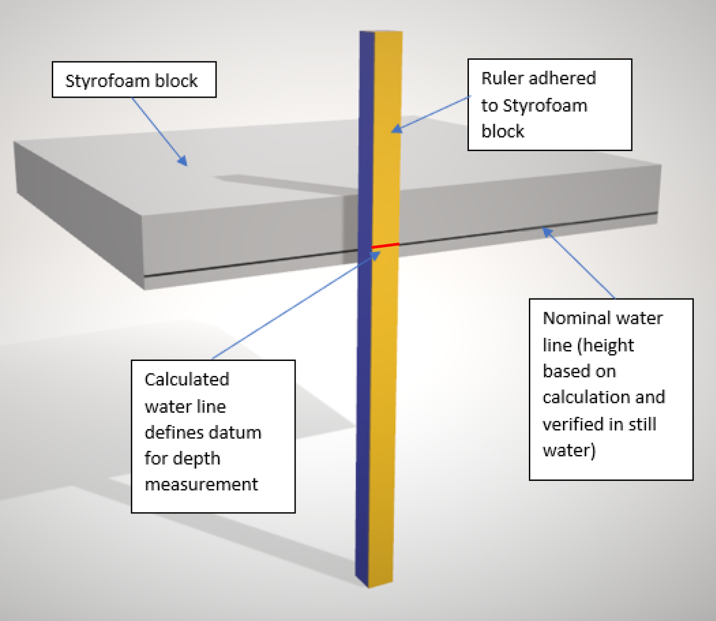
A lightweight, very buoyant, floating platform whose width and length are much larger than the wavelength of the surface undulations will “normalize” their effect and provide a more stable basis for depth measurement. The depth measurement will be between the nominal water line and the submerged fishing line—both of which should be relatively stationary.
6. Stinson offered two possible test locations. One is not valid because it is salt water. The other, the canal, is better but may also present its own challenges. The purpose of a canal is to move water, which begs the question: what is the flow rate of the water in this canal? If it is non-zero, then how does the moving water affect the hypothesis? If Stinson cannot answer these questions convincingly and control for their consequences, then a different site must be chosen.
7. Stinson should explain how he intends to find the midpoint of the line during the test.
8. Change the name of this experiment. “Torque” is never a factor in this test.
Bibliography
Bowden, G. (2004, October). Stretched Wire Mechanics. Geneva: CERN.
Certificates of Approval. (n.d.). Retrieved from National Measurement Institute, Australian Government, Department of Industry, Innovation and Science: https://measurement.gov.au/Publications/CertificateOfApproval/Pages/default.aspx
Feyrer, K. (2015). Wire Ropes. Berlin Heidelberg: Springer Verlag.
Shultz, K. (2018, January 08). What "Pound-Test" Means on a Fishing Line Label. Retrieved from Thoughtco website: https://www.thoughtco.com/fishing-line-pound-test-1310827ttps://www.thoughtco.com/fishing-line-pound-test-1310827
- - - - -
Here is Mitchel's response to the critique by Engineer Brian Dobbs
4th October, 2018
Dear Brian Dobbs,
Your recent critique was a great insight to the factors I have overlooked in the preparation to the “Torque the Line” experiment. I appreciate your time and effort in highlighting these issues in detail, and it will indeed empower me to have a far greater possibility of performing a conclusive experiment.
I value all feedback I receive, and I hold this critique in high regards coming from a Professional Engineer as yourself. The analysis of my values validate the theory behind this experiment and I am pleased to read you believe there is no reason this experiment will fail, if conducted carefully, documented thoroughly and reported honestly, all of which I intend to do.
I also appreciate and value review from “outside the echo chamber of flat earth fascism”. It was not my intent to only aim this experiment at the flat earth community, because I see the results of this equally as valuable to the mainstream science community looking to silence the “flat earth echo chamber”. By supporting an experiment which is already supported and funded by those in the flat earth community, it is a great opportunity to have a civil discussion between two opposing sides and agree on parameters for an experiment which both sides will agree on the outcome. Something which has not been achieved thus far.
I am simply looking for the truth, I am not holding onto any preconceived notions of the globe or flat earth so I do not categorise myself as being under one of those banners. The result of this experiment will be the first real step for me to prove to myself what the nature of the physical world around me is, through a physical measurement. But this will only be a personal belief I will then have and I can not put this belief onto others. It is paramount to have this experiment repeated and replicated elsewhere multiple times in order to form an objective truth. This is the goal of my experiment, to push others to question their world around them and prove to themselves what it is, and in doing so create an archive of physical evidence to be reviewed and analysed by all.
Response to “Torque the Line Experiment : A Critique”
by Brian Dobbs
Go fund me
As of 4th October 2018 the go fund me set up by myself, Mitchell Stinson, has recieved $981 Australian Dollars, raised entirely by those who believe we are in need of an experiment to prove the physical shape of the world around us.
This go fund me is primarily to fund the Spectra Braid that will be used in this experiment, and will be made available for anyone else who wishes to replicate the experiment elsewhere. If you are not familiar with how go fund me works, the entire amount of raised funds does not go directly to the person raising the funds. Go fund me takes around 10% of the money raised before forwarding the remaining 90% on to the person. That being said, the total amount for the Spectra Line was $925 NewZealand Dollars, which converted though PayPal was about $880 Australian Dollars the time of ordering the line.
Any extra amount raised is for equipment for the experiment, primarily the kayak or canoe, then for cameras etc. as stated in the go fund me.
Gravity
The assumption that one of the experiment’s goals is “to test whether gravity is real” is incorrect. The effect that we observe called “gravity” is real and undeniable , but what the cause and nature of “gravity” is still up for dispute, as widely stated by mainstream science.
I am merely questioning whether the “gravity” effect is the value of 9.8m/s2, and if it is correct in assuming this value for the calculation of the line sag and buoyancy. Which the experiment can cross check when the measurement of sag and buoyancy is conducted. If the values are found to differ from what has been calculated, then there is cause to question the value of 9.8m/s2. But I also recognise there are other factors that could cause the line to be buoyed up or sag more or less, such as wind moving the water, salinity content fluctuation, correct tension being applied etc.
Also the assumption that I take the stance of “flat earth and gravity are mutually exclusive concepts” is also incorrect. I do not believe that for gravity to be “real” the earth needs to be a globe. As stated above, mainstream science is yet to provide sufficient proof of the cause of gravity, so to say gravity only works on a globe is incorrect. There are many theories to the cause of gravity, but that is a topic for a different experiment.
Hypothesis
It has been noted that I have not provided a testable hypothesis for the experiment. Honestly, I can’t put my money on any outcome, as a physical mechanical test like this is yet to ever be attempted or recorded, so there is no precedence. But I am doing this experiment to prove the curvature of the earth correct, so if I was to hypothesis, it would be that the line will be submerged when run at water level across a tidally locked body of water, as is expected on a globe. Obviously there are many factors that can effect this and I have and will continue to evaluate them to set parameters for what will be categorised as a flat earth result or globe result.
Catenary Curve
The definition of a catenary is the curve that an ideal hanging chain or cable assumes under its own weight when supported only at its ends. The Archimedes' principle states that an object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.
This experiment will be conducted initially at water level, by which the entire span of the line will be supported by the buoyant force of the water, contradicting the very definition of a catenary curve.
Could Brian Dobbs please provide evidence that an “inverted catenary curve” can exist when being fully supported along the entire length of the line.
The experiment will then be repeated totally under the water at both ends at 5 inches depth, to show that buoyancy is not keeping the line on the surface of the water if it were to stay there during the initial test at water level. I understand Brian Dobbs has run his own calculations and has come to the conclusion that the salt water lake will not be suitable for the test, but I will address this later.
And finally, the experiment will be repeated totally out of the water at least 5 feet above water level on both sides, to show and measure the catenary curve. All, three of these results measured will be compared to the expected sag and buoyant values calculated and will determine the validity of the value of gravity given. With other factors taken into account of course.
Line Tension
I understand the breaking strength is not suitable in practice and will not be used. But I will be doing pre tests to determine the most suitable tension to use during the experiment. I will also consult with the manufacturer for a professional opinion.
Anchor Design
The only reason the dynamometer is not inline with the line itself is because the dynamometer is not waterproof, hence why it will be perpendicular to the main stretch on line and on a pulley to reduce friction. I understand this will give the dynamometer a false reading of true line tension, which is why I will be doing pre tests with the same rig over a short distance to determine a suitable reading from the dynamometer without breaking or overloading the line.
Regarding the method of tensioning the line with the come along I have not yet explained how I will do this, with elongation in mind. But that is not to say I have not thought of it.
My method will be as follows:
- • Barrels will be placed in the water at ether end
- • One side a barrel will be attached to a rope and anchored on shore to a steel steak
- • Spectra line will be attached to dynamometer, run through pulley, and run across to the opposite side of the lake
- • Spectra attached to dynamometer through pulley on second barrel at opposite side, where come along chain will be attached to barrel and rope running to another steel steak at the shore. This barrel will not be close to the shore, there will be approx 350feet of Rope between barrel and steak in order to use come along in increments to apply controlled tension to the line.
This method will account for the elongation of the line over the span between shores.
Also please note that water was never intended to be used for ballesting inside the barrels, only concrete.
Analysis of Calculations
I have already sent Brain Dobbs the excel spreadsheet which was used to calculate the values of sag and buoyancy. It will also be attached to this email. The calculations are available for review and verification, and show the salt water location will be suitable for the test, even when reduced to 50lb.
Please note, I may have used the term “neutrally buoyant” to describe the line in the videos, but it is clear in my calculations that I have taken into account the SG of the line being 0.98, and have therefore shown there will be a buoyant “lift” in the line.
Considerations
1) My hypothesis is as stated earlier.
2) Error propagation calculations will be undertaken and shown, best efforts will be made to measure the actual SG of the line
3) The line diameter shall be measured before and during stress
4) Water density and temperature will be measured before test
5) The styrofoam with ruler attached method of measuring will be used
6) The salt water lake will still be used and the totally submerged test will indicate if there is more buoyancy than was calculated for and taken into consideration. The fresh water site canal leads to a waterfall which runs when the lake is too full, and will be used. Other fresh water sites have also been found and will be also considered to repeat test in.
7) Mid point will be found using GPS and marked with paint to be found easily again
8) The “torque” refers to the come along which is applying force to “the line” so the name will stand, as this isn’t vital to the outcome to the experiment
I thank Brian Dobbs for his critique and analysis and expect there will be a response to this response document.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Published on – September 13, 2018
Discussion at - https://www.youtube.com/channel/UC7ipUKERU0tzYFxALJBli4A/discussion
Our home page all articles - http://flatearthlunacy.com
kind regards, JonahTheScientist