Main Menu

Search

Introduction

Dear Visitors,                                                                                                                                    April 21, 2017

Thank you for stopping at FlatEarthLunacy.com

As a scientist with college degree in Astronomy, minor in Physics and Mathematics, I was appalled to find folks telling outright falsities and presenting bad science to bolster suspicion of our known accepted reality - that the Earth is a beautiful blue globe.

This blog clearly shows scientific proofs that debunk everything that flat Earth proponents claim.  Here we also expose the comments those YouTube video channels delete, because they don't want you to see them.

The Earth is not flat.  That claim is a conspiracy theory perpetrated by ignorant people who have ulterior personal motives and agendas.

The Earth is a beautiful blue spheroid globe spinning on an axis 23.5° once each day, and orbiting the Sun every 365.25 days.

   JonahTheScientist.png

  

kind regards,  Jonah The Scientist


(This email address is being protected from spambots. You need JavaScript enabled to view it.)                 © FlatEarthLunacy.com (2015 - 2022) - All rights reserved

Get notified of new articles on Twitter / Facebook - twitter.com/FlatEarthLunacy , facebook.com/flatearthlunacyofficial   

JonahTheScientist SALES / Recommendations: STEM (Science, Technology, Engineering and Math) science projects for young adults, and science books for everyone.  Enjoy! 


Here is a list of our copyright and USPTO Legal Trademarks:

Trademark of name “Jonah The Scientist”
Trademark of name “Flat Earth Lunacy” 
Trademark of logo of “Jonah The Scientist”
Copyright of artwork at the US Library of Congress, for “JonahTheScientist Official Logo”
In any word combination, script, color, or word separation by blanks or other characters.

Our internet blog/web sites are exclusively licensed to FlatEarthLunacy.com, twitter.com/FlatEarthLunacy, facebook.com/flatearthlunacyofficial AND https://www.youtube.com/channel/UC7ipUKERU0tzYFxALJBli4A/discussion.

Our articles and screen shots authorized under - Copyright Disclaimer Under Section 107 of the Copyright Act 1976.  Allowance is made for "fair use" for purposes such as criticism, comment, news reporting, teaching, scholarship, and research.
Section 107 of the U.S. Copyright Act states: “Notwithstanding the provisions of sections 106 and 106A, the fair use of a copyrighted work, including such use by reproduction in copies or phonorecords or by any other means specified by that section, for purposes such as criticism, comment, news reporting, teaching (including multiple copies for classroom use), scholarship, or research, is not an infringement of copyright.” This internet site may contain certain copyrighted works that were not specifically authorized to be used by the copyright holder(s), but which we believe in good faith are protected by federal law and the fair use doctrine for one or more of the reasons noted above. 

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 

 

Mr. Mark Sargent, the Earth is not stationary. Try this easy junior high school experiment yourself to find out the reality.



- - - 

NOTICE of April 27th: Mark has already deleted our invitation to do this experiment.  By deleting this comment, Mark is also now complicit in hiding reality from his YouTube audience.  


   2019-04-27_16-20-03.png

- - - 

Dear Mr. Sargent,

An easy experiment for any young adult (14+) to prove that the Earth moves and is orbiting the Sun.

Mark, before you say that the planet Jupiter is a light in the sky and there is nothing there to land on, think again.  A small telescope reveals that Jupiter is large, round and rotates.  Satellites revolve around it.  Why do you adhere to the same denial as the clergy who sentenced Galileo to death?  You are lost and live in your own world of make believe, afraid to accept reality.

All you need is:
A small telescope (3-inches or larger)
A stop watch
Ephemeris listing of Jupiter moon eclipse times
Math skills such as adding, subtracting, dividing and multiplying
The ability to read and understand what you read

The experiment:
The four major moons of Jupiter are easily seen with a 3-inch telescope.  They look like bright stars.
Consult the Ephemeris for the time that a moon will be eclipsed (enter the shadow of Jupiter and disappears from your telescope view).

20 minutes before the eclipse take your telescope outside and point a Jupiter.  Focus the eyepiece to see Jupiter and the moon(s). Since the four moons of Jupiter are always in rotational orbit around the planet, at any given time you may see one or several. 

Watch the eclipse and determine the time the moon disappeared from view as it enters Jupiter's shadow (you no longer see it).  Start your stopwatch when the moon disappears and then reference that to Coordinated Universal Time site to get the actual Universal Time of the eclipse event.

Record the time and date of each event in a notebook.

Continue for 6-month to observe as many eclipses as weather permits.  Best to start your experiment on a date that the Earth is closest to Jupiter, and end the experiment on a date when the Earth is farthest from Jupiter.  Consult the Ephemeris listed below.

How does this work?
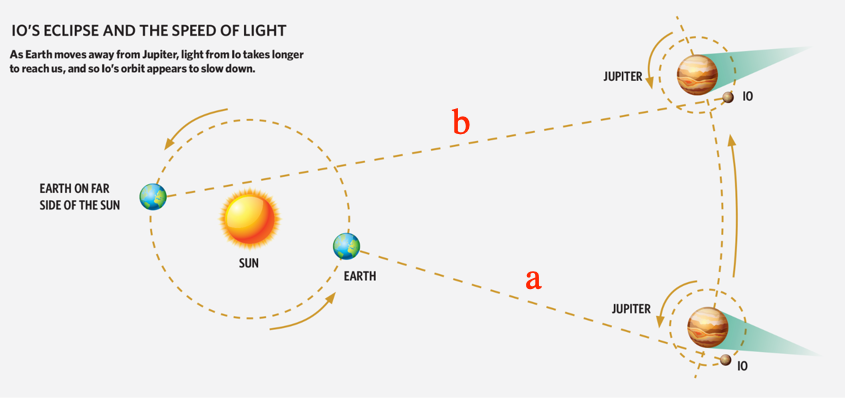
Referring to the photo below, determine the eclipse time at distance (a).  Calculate when you should see the next eclipse at distance (b).  You will find that the eclipse at distance (b) occurs minutes later than the predicted time.  That is because light now has to travel a further distance to get to the Earth, (b) - (a) = x miles further away. 
Since distance = velocity * time,  we can also write this as ... 
distance change between the earth and Jupiter = speed of light * time [between calculated and observed eclipse at point (b).]       
Since you actually observed the eclipse to occur later than predicted, that proves the Earth moved between the time of eclipse (a) and eclipse (b).  YES.  You have now proved earth movement around the Sun.    

This is a reproduction of the Ole Roemer experiment conducted in 1676, the first successful determination of the speed of light.  Galileo tried in 1638 using lanterns on two different mountain peaks, but did not get a number.  However, Galileo did conclude that the speed of light was at least several times faster than the speed of sound.

Do this experiment for each of the four large moons of Jupiter.

"I did this experiment myself in 1971 - 1972 and got accurate results," JonahTheScientist

- - -

   2019-04-17_23-58-52.png


- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 


   2019-04-20_16-23-22.png


After all observations are done, it's time to analyze the data and come up with the results.

1.  Find two dates when Jupiter and earth are far and near, preferably about two to three months after Jupiter is in conjunction and about a month before Jupiter is at opposition These conditions ensure that Jupiter’s shadow is to the east of the planet so that eclipses are easily seen.

The Far Date and Near Date for this example are:

Near Date =     May 10, 2019   (about a month before opposition)

Far Date =      March 12, 2020   (about 2.5 months after conjunction)

10 Jun 2019   –  Jupiter at opposition
14 Jul 2020   –  Jupiter at opposition
19 Aug 2021   –  Jupiter at opposition
26 Sep 2022   –  Jupiter at opposition



- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 

2.  Observe and time an eclipse of Io on the Far Date

(the eclipse happens at the moment Io moves into Jupiter’s shadow). If there is no eclipse on your Far Date, there will be one the next day – observe that one.)

OBSERVING TIPS:

  • Set the magnification view to 400x and use the ID Colors to identify Io.
  • Turn on the “Top View” to see where Io is with respect to the position of Jupiter’s shadow.
  • When Io is more than one Jupiter disk away from the planet’s edge, set the Observing Interval to 0.5 hour.
  • Use the Next button to advance the observations.
  • When Io is one Jupiter disk away from the planet’s edge, set the Observing Interval to 0.01 hour. Advance a few steps…
  • When Io is about one quarter of a Jupiter disk away from the planet’s edge, set the observing interval to 0.005 hours.
  • Gradually advance time, step by step, until the moon just disappears---this is the start of the eclipse.

Time of the Far Date Eclipse

Standard Format:         March 1, 2008     18h  07m  18 sec

Julian Day:                  2454527.255069

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 

3.  Estimate how many orbits Io will make from the Far Date to the Near Date

Number of Orbits   =    (Far Date – Near Date) / Synodic Period of Io

Synodic Period of Io = 1.769861 days

Number of Orbits   =    (May 31, 2008 – March 1, 2008) / 1.769861 days per orbit

Number of Orbits   =    91 days / 1.769861days per orbit                                =    51.42 orbits

Round the value down to a whole number of orbits:

Number of Orbits   =    51 

Note: This is the number of orbits Io will make to go from the first eclipse on the Far Date to the predicted eclipse at the Near Date

 
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

4.  Calculate the time interval from the first eclipse to the predicted eclipse

Time to Predicted Eclipse     =    Number of Orbits x Synodic Period of Io (don’t round off the period—keep as many decimal places as you can)

Time to Predicted Eclipse     =    51 orbits x 1.769861 days per orbit

                                                         =    90.262904 days


- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

5.  Calculate the JD of the predicted eclipse at the Near Date:

Predicted Eclipse Time     =    Far Eclipse Time (JD) + Time to Predicted Eclipse

Predicted Eclipse Time     =    2454527.255069  +  90.262904

                                         =    2454617.517973

 
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

6.  Observe the predicted eclipse

Advance the simulation to a few hours before the Near Date eclipse. Starting your observations before the predicted eclipse is a key part of getting good data. The reason for this is that you expect the near eclipse to occur several minutes before the predicted time, and you don’t want to miss it. If you miss it, and observe the next eclipse, several days later, you won’t get the right speed of light.  So, just to be on the safe side, let’s start our observations 0.1 JD, or 2.4 hours, before the predicted eclipse time.  In other words, since the predicted eclipse time is Julian Day 2454617.517973, we start our observations on Julian Day2454617.417973. Then slowly advance the time to catch the predicted eclipse a few minutes before your predicted time.

Observe and time the eclipse of Io that happens on this Near Date

Observed Eclipse Time (JD)   =    2454617.508208

 
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -


7.  Find the time difference between the predicted eclipse and the observed eclipse

Time Difference             =    Observed Eclipse Time (JD) – Predicted Eclipse Time (JD)

Time Difference             =    2454617.508208  –  2454617.517973

                                       =    – 0.009765 days

Time Difference (ΔT)     =    – 14.1 minutes

Note: The negative value indicates the eclipse occured before the predicted time.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

8.  Find the change in distance between Jupiter and earth from the Far Date to the Near Date

Distance (au) of Jupiter from Sun (March 1)       =    5.71785 au

Distance (au) of Jupiter from Sun (May 31)        =    4.39149 au

Change in distance     =    March 1 distance – May 31 distance

Change in Distance (ΔD)    =    5.71785 au – 4.39149 au

                                            =    1.32636 au


- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

9.  Calculate the Speed of Light

Speed of Light    =    ΔD / ΔT

Speed of Light    =    1.32636 au / 14.1 minutes

                           =    0.094327 au / minute     

Convert this value in au / minute to the more familiar meters / second

Speed of Light    =    2.34 x 108 m/s


- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

10.  Compare your value to c

Find the Percent Difference between your calculated value of the Speed of Light and the accepted value, c = 3.00 x 108 m/s

Percent Difference    =    [ (Speed of Light – c) / c ] x 100%

Percent Difference    =    [ (2.34 x 108 m/s – 3.00 x 108 m/s) / 3.00 x 108 m/s ] x 100%

                                 =    [ – 0.64 x 108 m/s / 3.00 x 108 m/s ] x 100%         

                                 =    – 21%

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Reference:

Jupiters Moons and the Speed of Light.  Get here the "Student manual For the Roemer experiment (MS Word format) 
http://www3.gettysburg.edu/~marschal/clea/roemerlab.html

- - - 

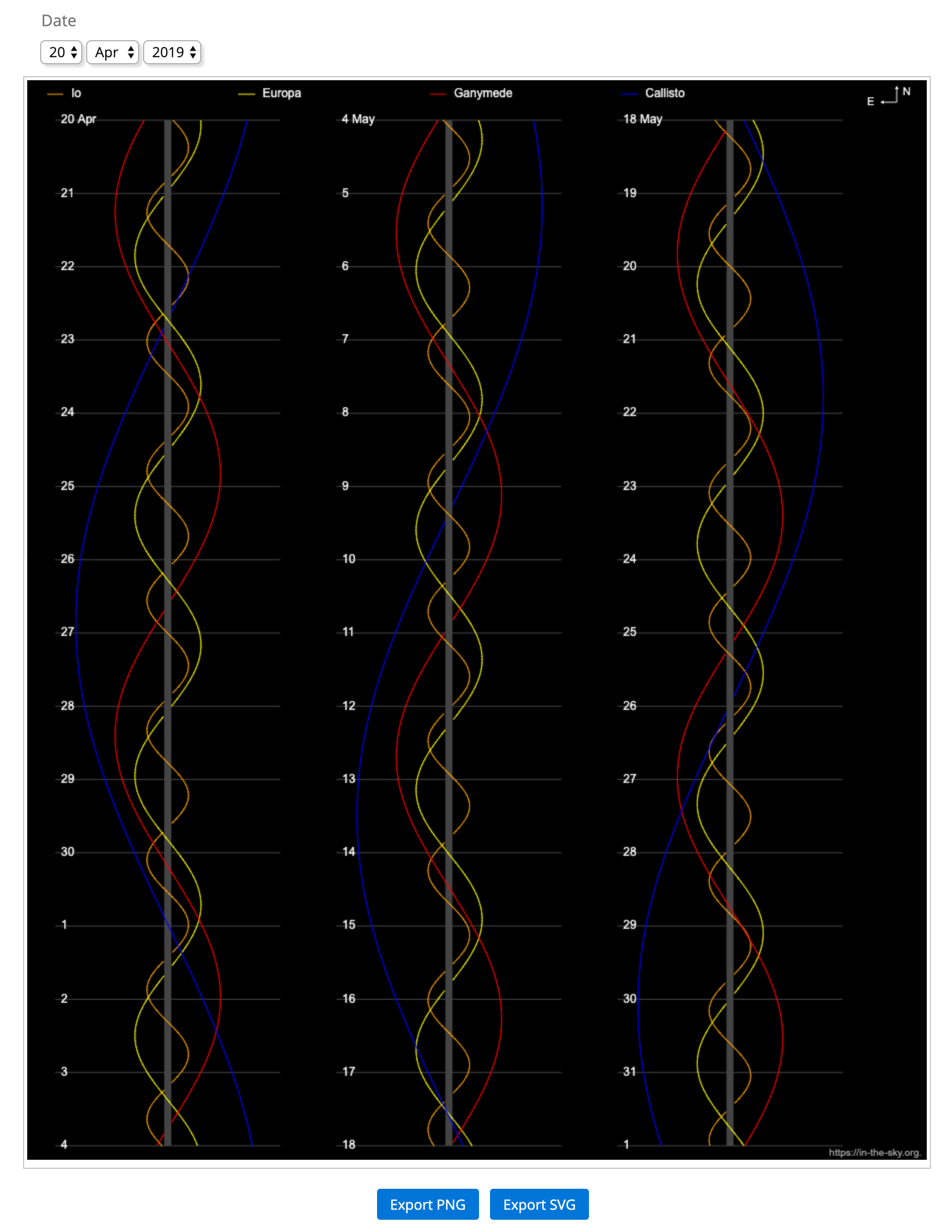
The following chart shows the position of the large 4 moons of Jupiter (Io, Europa, Ganymede and Callisto) with respect to the planet itself when you look at it through your telescope.

Before you go outside to observe Jupiter, consult this chart.  Set the date for today. 

(https://in-the-sky.org/jupiter.php)


   2019-04-20_16-43-49.png


   2019-04-20_16-44-51.png


   2019-04-25_00-00-56.png





- - -

Coordinated Universal Time
https://time.is/UTC

Geocentric Ephemeris for Jupiter : 2019
http://astropixels.com/ephemeris/planets/jupiter2019.html

 
https://s22380.pcdn.co/wp-content/uploads/WebJphenTab2019.pdf

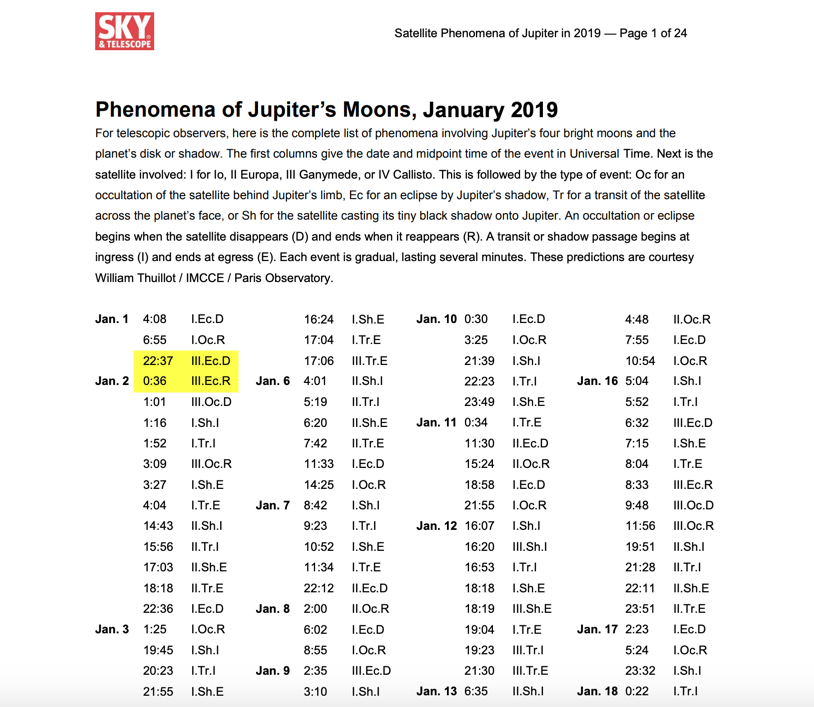
   2019-04-17_01-14-14.png

- - - 





Published on – April 24, 2019

Discussion at - https://www.youtube.com/channel/UC7ipUKERU0tzYFxALJBli4A/discussion

Our home page all articles - http://flatearthlunacy.com

kind regards, JonahTheScientist